On the Hydrodynamics of Bus Boarding and the Theory of Knots
Roy Lisker, 1996
It is late at night. Imagine that we are standing on the loading dock of a bus terminal situated in the downtown area of some major city - "we" meaning a crowd of about 50, imbued with some notion of a linear ordering, although it may appear to be randomly distributed around an empty bus. It's been a long, hot, stressful summer day. The ambient mood is irritable, impatient. Public transportation in America has reached an all-time low, and people are fed up.
A sallow, well-groomed businessman has adopted a defensive posture and avoids contact with others. A shabby drunk tries to strike up conversations without success. A survey would show that most of us are concerned only with getting onto the bus as soon as possible, dropping into a seat and getting some sleep.
With the demise of Trailways in the mid 80's, the bus is probably a Greyhound, though it could also be Peter Pan, or Peerless, or Connecticut Limousine, or Bonanza . No matter: the trajectories presently to be subsumed apply to all buses of a certain height, length, width and construction.
Our bus came in half an hour behind schedule; then it had to be withdrawn from circulation for cleaning and minor repairs. A new driver appeared; there were further delays because of paper work, perhaps some misunderstandings with the central headquarters in Dallas. Let's assume that it's an hour and a half after the scheduled departure time. Finally a dulcet voice, tinged with doomsday, comes over the loudspeaker and announces that the bus is ready for boarding.
As a collective sigh of relief, so strong that it is virtually visible, rises from the crowd, our bus, newly serviced, straining in harness like a well-groomed horse eager for the journey, emerges from the shed and enters its stall. The driver opens the door from inside, steps down onto the loading dock and begins collecting tickets.
This is the initial terminus of this particular route, there are no persons in transit waiting to reclaim their seats. The bus is void, ripe for invasion. The colloidal mass of passengers whips into a linear spine and begins to slouch forward into the bus.
STAGE A
Our working assumption is that it is the normal American tendency (and among other industrialized cultures) for people to want to sit with their friends or families, or else sit alone. Since people in general, (though not invariably) , also prefer to sit by the window, a sensible model conformable to many situations encountered in the real world can assume that, barring the presence of family or friends - later they may be factored in as first or second order perturbations - the first wave of passengers will spread out through the bus in a search for unoccupied ranges . By a range we mean one of the units against the walls consisting of one pair of seats stuck together in close proximity. There is also a 3-seat range at the far end of the bus to the right of the bathroom. A Greyhound bus normally holds seats for 47 passengers ( Note: this article was written circa 1996. Certain dimensions have changed but the underlying conclusions are the same),that is to say 23 ranges.
Under this set of initial conditions, Stage A comes to an end when the first wave of 23 passengers have occupied the window seats in all the ranges.
STAGE B
For convenience sake we now introduce 3 new assumptions. These reflect naturally occurring situations that are commonly found in what one may call canonical bus boarding configurations:-
The interior of the bus is in near total darkness, save perhaps for reflected light coming in from the platform , which itself is illuminated by only a few spotlights.
-
(The seats have high backs, with the result that people of normal height can't tell if the window seat of a range is occupied until they are almost level with, or at most 2 ranges distant from it.
-
The fact that more people are waiting to board the bus than there are seats is not well understood by anyone.
People at the entrance continue to stream in through the front door of the bus, turn to the left and proceed down the corridor in search of a seat. Because we have assumed that most unaccompanied people prefer to sit by the windows, the passengers of stage B will continue shuffling down the narrow corridor until, in spite of the constraints of assumptions 1 to 3 , they realize that every range in the bus holds at least one occupant.
This recognition always occurs in a tiny region which we identify as the "critical point", or "C.P." for short , and is usually located between 0.75 and 0.8125 of the way down the full length of the bus . Beyond it lie two ranges on the left, two on the right, and the 3-seater at the back still remaining, for a total of 11 places, 5 of which, from stage A, are filled.
The first individuals to reach the critical point may now want to turn back, only to discover that it is too late to do so: a hoard of angry passengers blocks their way. This compels those now at the head of the line to take some kind of immediate action.
They will therefore begin settling into whatever seats they find immediately at hand, starting with the ones just beyond the critical point, up to the back wall. Observe that the seating will tend to unfold in reverse order: the seats at the critical point being occupied first, then the next, and finally the two worst seats in the bus, in the 3-seater. Stage B now comes to an end when the upper quarter of the bus is totally occupied. Between it and the contribution of stage A, 29 seats have now been filled.
Theorem
If the number of occupants of a 47 seat Greyhound is in the neighborhood is 33, ( or less ) , then the chances of having a range entirely to oneself are greater for persons who grab a seat at the front of the bus, than for those in the middle or back.
Proof:
People entering a bus where visibility is poor will tend to lurch down the aisle in search of window seats. Only at the critical point will they realize the futility of their quest. Those at the head , being obstructed by the phalanx of persons behind them in search of the same thing, will be unable to retrace their steps and will take the first seats at their disposal. Assuming that this process extends to the set of ranges just below the critical point, we obtain a figure of:
23(from stage A)
+ 6 (above C.P .)
+ 4(below C.P.) = 33. Q.E.D.
STAGE C
Given that the remaining passengers continue to maintain their relentless march to the critical point, the result must inevitably be:
****** CHAOS!! ******
Pushing, cursing, shouting, biting, shoving, ramming, the incoming passengers riot for the remaining 13 to 17 seats. The hydrodynamic contest, under the action of mutually opposing forces, rolls in waves of turbulence which, taking on an identity of its own, crests back and forth through the corridor in a dizzying and malevolent dance. An irate mother, her two children in tow, her wide suitcase aggressively wielded before her, marches righteously up the corridor. The taciturn businessman who regrets his decision to consort with the lower classes in a vehicle of this sort, chops his tightly rolled Wall Street Journal on the heads and shoulders of adjacent strangers. The drunk, now midway to the critical point, is whirled back and forth, until some compassionate soul crams him into a seat for his own good. Midst all the confusion of crushed and dispersed luggage, kicked shins, torn clothing and, alas, even perhaps a few blackened eyes, ( hopefully with a few dedicated practitioners of non-violence in their ranks ), the entire contingent will eventually be seated, the driver free to swing into his saddle and sally forth .
Theorem
Even through most of stage C, it is still a good idea for the passengers of stage A to grab a seat at the front.
Proof:
The turmoil generated by stage C more or less guarantees that someone pushing back through the line will take the very first seat available to him. Those coming up from the entrance will not yet realize that there are no more seats to be had at the back and will continue their relentless advance. Q.E.D.
It turns out that this pathology, stage C in particular, can be diagnosed by certain tools of mathematics natural to the modern theory of knots, links and braids. In this last decade this subject has swollen to immense proportions, as one scientific discipline after another discovers that its knottiest problems may literally be untied. Here, in quick sketch we present a few of the elementary concepts from this field, just enough to suggest the flavor of such an approach to the problems of bus boarding:
Rudiments of Knot Theory
A Knot is a closed loop in normal 3-dimensional space which, in the general case, cannot be untwisted into a simple O-ring, that is to say, flattened into a circle. This is also considered to be a special knot known as the trivial knot or, more commonly,the Unknot.
A Link is a collection of knots. In a one-component link, the knots are inseparable. The Ballantine Rings are an excellent example of a 1-component link: each pair of loops is "unlinked", but the 3 of them together cannot be separated:

The simplest non-trivial knot is called the Trefoil , and looks like this:

A Braid is a collection of N strands in 3 dimensional space extending from a set of N initial points to N terminal points. As a braid can also be seen as a knot that has been cut through at a certain place, and since a knot can always be formed out of a braid by connecting up the initial points with the end points in a certain way, Braid Theory and Knot Theory are interchangeable, although there is considerable difference in the approach.
Although real knots exist only in 3-dimensional space, it can be mathematically demonstrated that all knots are equivalent to their shadows, or 'knot diagrams' projected onto a plane, provided one labels the under- and over-crossings at the self-intersections of the diagram , and takes care that the projection of one intersection does not fall directly on top of another. A single object casts many shadows: the same knot can project into many diagrams. The equivalence of all the diagrams of the same knot is known as "ambient isotopy": 2 knot diagrams are ambient isotopic if they come from the same knot. It was shown in the 19th century that any two ambiently isotopic knot diagrams X and Y can be transformed into each other by the application of 3 alterations, known as Reidemeister Moves . These are:
-
Untwisting (twisting) a loop:
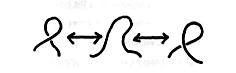
-
Drawing unlinked strands apart (together):
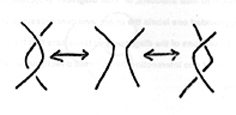
-
Moving a strand, lying beneath two others and above an intersection, to a place below the intersection:

-
Limited space does not allow for more details, except to say that the 3rd Reidemeister move is related to something from statistical mechanics known as the Yang-Baxter Equation. The marriage of 'Reidemeister' with 'Yang-Baxter' has spawned some of the most horrific symbolic calculations known to mankind. They are not entirely useless, and turn out to have some applications to the statistical mechanics of melting ice.
Example: one can easily show through the application of the 3 Reidemeister moves, that the following configuration is equivalent to the Unknot:
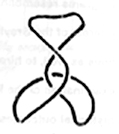
The central problem of Knot Theory is to decide when two knot diagrams represent the same knot. This can be very difficult, and several classical polynomials, known as "knot invariants", have been developed to deal with large classes of diagrams: the Alexander and Alexander-Conway polynomials, the Jones polynomial, the Kauffman polynomial, the Homfly polynomial, and so on.
Two polynomials associated with different knots must be different. However, the same knot may be associated with different polynomials. To date, no-one has discovered a universal invariant that is unique for each knot. Let's put it this way: there is a way, via tensor calculus, to generate an invariant that is unique to each knot. It is about as useful to knot theorists as writing down the atomic structure of one's toes is for someone learning how to walk.
There are several ways by which the 3 stages of the bus boarding process can be represented through schematic diagrams resembling knots and braids . It would be in the interest of the Greyhound corporation, and perhaps other bus lines as well, to hire knot theorists to decide, from an examination of the knot, link and braid diagrams of all historical outcomes of stage C of the bus boarding process, which of them are generic in the sense that they are most often reproduced. With this information at hand Greyhound would then be in a position to issue insurance policies against injuries , like damaged luggage and broken limbs, arising from the vagaries of stage C.
One such scheme I have dubbed a "tangle box". It preserves the basic shape of the bus but provides no information on the temporal relations. Another, the "confrontation graph" , maps the long axis of the bus against time.
I. Representation of the bus boarding process through Tangle Boxes
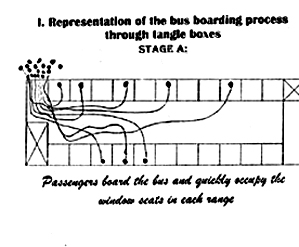
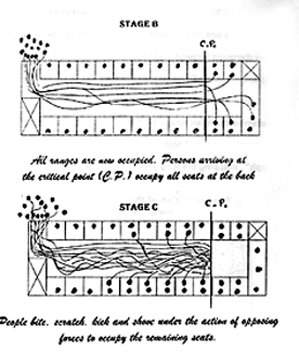
Tangle box pictures are suggestive at best. In the absence of the time dimension the self-intersecting paths on them have no ready interpretation.
II. Confrontation Graphs
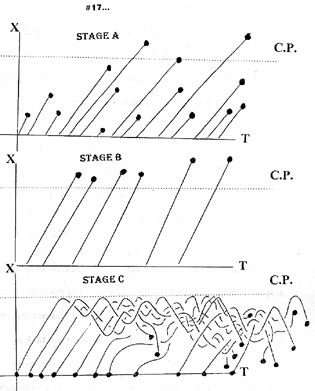
These provide more information. The graph of stage C is a braid diagram. We adopt the following under/over-crossing convention : An overcrossing of trajectory X with trajectory Y shall be interpreted to mean that X, moving either forward or back, cuts across Y's path or pushes him out of the way.
Our schematics are not adequate to deal with situations in which X actually drags Y down the length of the bus, or even ejects him altogether! This may be represented as follows:
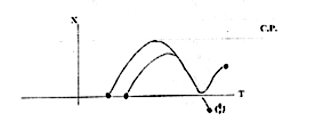
Diagrams of this sort lie outside the purview of both knot and braid theory.
Although convinced that the Greyhound corporation ought to take a keen interest in my latest researches in this domain, I have not, despite many years of experience with these phenomena, proposed myself for the task of applying knot invariants to the uncovering of the generic configurations of stage C. The weakness of my geometrical intuition precludes my doing so.
One should not doubt that the brilliant modern school of young knot theorists will prove themselves more than equal to the task , as well as far more daunting challenges that must arise in the future.
Return to
Home Page